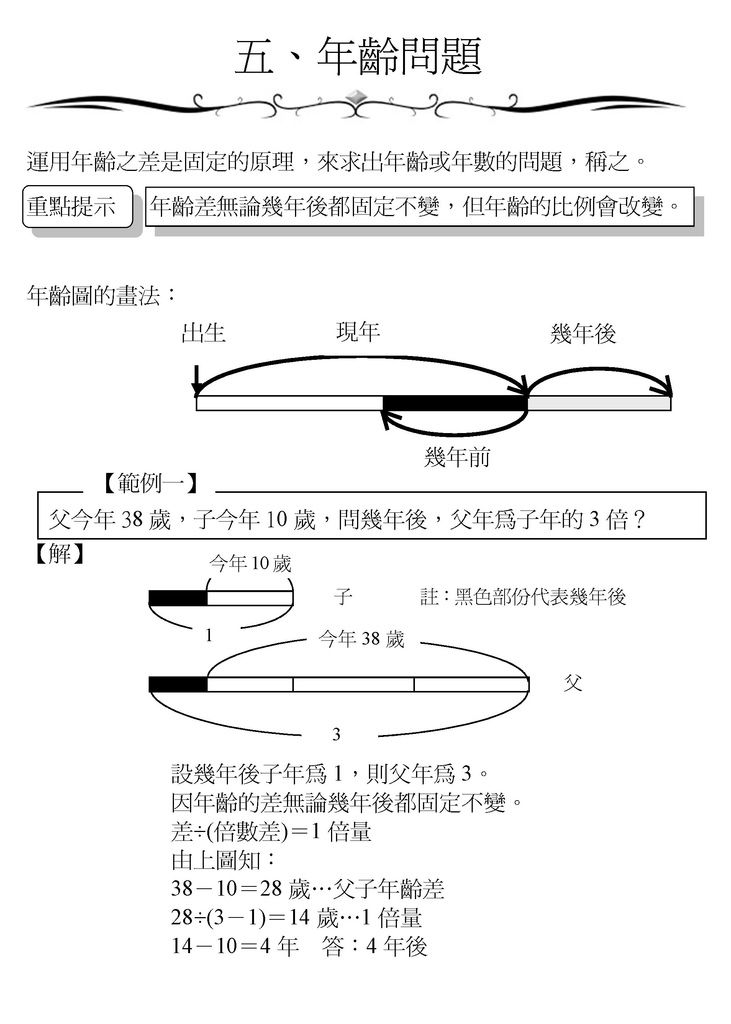
年齡與倍數問題的數學解題技巧主要圍繞「年齡差不變」和「倍數關係變化」兩大核心概念,並且常用「線段圖」和「代數方程」來輔助理解與計算。以下是具體技巧與步驟:
1. 理解年齡差不變的原則
- 年齡差(兩人年齡的差值)是固定不變的,無論過了多少年,兩人的年齡差都不會改變。
- 例如,媽媽和孩子的年齡差是22歲,10年後仍然是22歲。
2. 利用倍數關係設定方程
- 倍數關係指一個人的年齡是另一個人的幾倍。
- 設較小年齡為基準量(如孩子的年齡為1份),較大年齡為比較量(如媽媽是3倍,即3份)。
- 年齡差 = 基準量 × (倍數 - 1)
- 透過這個公式,可以求出基準量(較小年齡):
[ \text{基準量} = \frac{\text{年齡差}}{\text{倍數} - 1} ] - 例如,姐姐和妹妹相差12歲,姐姐是妹妹的3倍,妹妹年齡 = 12 ÷ (3-1) = 6歲,姐姐則是18歲。
3. 使用線段圖輔助理解
- 畫出兩人的年齡線段,較小年齡為一段,較大年齡為倍數倍長的線段。
- 標示出年齡差,幫助視覺化問題,便於推算。
4. 注意倍數隨時間的變化
- 雖然年齡差不變,但倍數會隨時間改變,因為兩人年齡都在增加。
- 例如,當孩子年齡增加,媽媽年齡是孩子的倍數會逐漸減少。
5. 解題步驟總結
- 步驟一:找出年齡差(固定不變)。
- 步驟二:根據倍數關係,設基準量與比較量。
- 步驟三:利用公式計算基準量(較小年齡)。
- 步驟四:求出另一個人的年齡。
- 步驟五:檢查倍數是否隨時間變化,理解問題背景。
這些技巧適用於小學中高年級的年齡與倍數問題,能幫助學生建立清晰的數學模型和解題思路。若需要更深入的練習,可以參考相關教學影片與教材。